Hamming Codes
Hammming Code - (7, 4)
I will use the Galois Field library to implement the Hamming Code. The library can be installed using pip.
pip install galoisLet’s import the library and numpy.
import numpy as np
import galois
from scipy import linalgLet’s define the generator matrix for the Hamming Code. The generator matrix is defined as follows:
\[G = \begin{bmatrix} 1 & 0 & 0 & 0 & 1 & 0 & 1 \\ 0 & 1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 0 & 1 & 1 \\ \end{bmatrix} = \begin{bmatrix} I_4 & P \end{bmatrix}\]basis = np.array([[1, 0, 0, 0, 1, 0, 1],
[0, 1, 0, 0, 1, 1, 0],
[0, 0, 1, 0, 1, 1, 1],
[0, 0, 0, 1, 0, 1, 1]], dtype=int)n = 7 # Length of codeword
k = 4 # Length of message vectorTo encode a message vector \(\underline{m}\), we take the dot product of the message vector with the generator matrix.
\[\underline{c} = \underline{m} \cdot G\]message = np.random.randint(2, size = k, dtype='int') # Generate random message
encoded_message = np.mod(np.dot(message, basis), 2) # Encode the messageErasure channel erases some random bits from the codeword. Let’s define the erasure channel.
noise = np.random.choice([0, 'e'], size=(n,), p = [1 - p, p]) # Add noise to the codeword
y = np.array(['e' if noise[indx] == 'e' else encoded_message[indx] for indx in range(n)])Okay! But now how do we decode the message? Since \(\underline{c}\) is a codeword, it must be in the span of the generator matrix. So, we can write \(\underline{c}\) as a linear combination of the columns of the generator matrix. When erasure channel erases some bits, we can still write the received codeword as a linear combination of the columns of the generator matrix. Let’s define the received codeword as \(\underline{y}\). We will erase the columns of the generator matrix corresponding to the erased bits and will find a full rank matrix. We will then find the inverse of the matrix and multiply it with the received codeword to get the message vector. Let \(G'\) be the matrix with the erased columns removed. Let \(\underline{y'}\) be the received codeword with the erased bits removed. We can write \(\underline{y'}\) as follows:
\[\underline{y'} = \underline{m} \cdot G' \implies \underline{m} = \underline{y'} \cdot (G')^{-1}\]We will need the full rank matrix to find the inverse. Let’s find the full rank matrix.
def find_linearly_independent_columns(matrix):
rows, cols = matrix.shape
basis = matrix.copy()
num_independent_cols = np.linalg.matrix_rank(basis)
linearly_independent_indices = []
i = 0
while np.linalg.matrix_rank(basis) >= num_independent_cols:
# Remove the i-th column from the basis matrix
reduced_basis = np.delete(basis, -i - 1, axis=1)
# Check if the reduced matrix is full rank
if np.linalg.matrix_rank(reduced_basis) >= num_independent_cols:
basis = reduced_basis
else:
i += 1
if i >= basis.shape[1]:
break
# Remove excess rows/columns to make the basis matrix square
if basis.shape[0] > basis.shape[1]:
basis = basis[:basis.shape[1], :]
elif basis.shape[1] > basis.shape[0]:
basis = basis[:, :basis.shape[0]]
basis_matrix = basis # set the final matrix
# Find the corresponding indices in the original matrix
linearly_independent_indices = np.array([index for index, column in enumerate(matrix.T) if any(np.array_equal(column, basis_col) for basis_col in basis_matrix.T)])
return linearly_independent_indices, basis_matrixNow we are ready to decode the message.
class BECDecoder:
def __init__(self, n : int, k : int):
self.n = n
self.k = k
self.dim = self.k
self.basis = np.array([[1, 0, 0, 0, 1, 1, 1],
[0, 1, 0, 0, 1, 1, 0],
[0, 0, 1, 0, 1, 0, 1],
[0, 0, 0, 1, 0, 0, 0]], dtype=int)
self.GF = galois.GF(2)
def decode(self, recievedCodeword: np.ndarray) -> np.ndarray:
erasedBasis = np.delete(self.basis, np.where(recievedCodeword == 'e')[0], axis=1)
erasedCodeword = np.delete(recievedCodeword, np.where(recievedCodeword == 'e')[0])
if np.linalg.matrix_rank(self.GF(erasedBasis)) < erasedBasis.shape[0]:
keep_indices, erasedBasis_sqr = find_linearly_independent_columns(self.GF(erasedBasis))
erasedCodeword = self.GF(np.array([erasedCodeword[indx] for indx in keep_indices], dtype = int))
erasedBasis_sqr_inv = erasedBasis_sqr.T @ np.linalg.inv(self.GF(erasedBasis_sqr @ erasedBasis_sqr.T))
finalDecodedMessage = erasedCodeword @ erasedBasis_sqr_inv
return self.GF(np.pad(finalDecodedMessage, (0, self.dim- len(finalDecodedMessage)), mode='constant'))
keep_indices, erasedBasis_sqr = find_linearly_independent_columns(self.GF(erasedBasis))
erasedCodeword = self.GF(np.array([erasedCodeword[indx] for indx in keep_indices], dtype = int))
erasedBasis_sqr_inv = np.linalg.inv(self.GF(erasedBasis_sqr))
finalDecodedMessage = erasedCodeword @ erasedBasis_sqr_inv
return finalDecodedMessageLet’s test the decoder.
n = 7
k = 4
p = 0.1
basis = np.array([[1, 0, 0, 0, 1, 0, 1],
[0, 1, 0, 0, 1, 1, 0],
[0, 0, 1, 0, 1, 1, 1],
[0, 0, 0, 1, 0, 1, 1]], dtype=int)
# Generate random message
message = np.random.randint(2, size = k, dtype='int')
# Encode the message to get the codeword
encoded_message = np.mod(np.dot(message, basis), 2)
# Add noise to the codeword
noise = np.random.choice([0, 'e'], size=(n,), p = [1 - p, p])
y = np.array(['e' if noise[indx] == 'e' else encoded_message[indx] for indx in range(n)])
decoder = BECDecoder(n, k)
decoded_message = decoder.decode(y)
print("message", message)
print("encoded_message", encoded_message)
print("y", y)
print("decoded_message", decoded_message)
print("error", (GF(message) + decoded_message))Let’s plot the error rate vs the probability of erasure.
from numba import njit, prange
import matplotlib.pyplot as plt
from tqdm.auto import tqdm
GF = galois.GF(2)
nSym = 10**2
pVec = np.arange(0.9, 0.00, -0.05)
e_vec_bec = {}
generator = np.array([[1, 0, 0, 0, 1, 0, 1],
[0, 1, 0, 0, 1, 1, 0],
[0, 0, 1, 0, 1, 1, 1],
[0, 0, 0, 1, 0, 1, 1]], dtype=int)
rate = k / n
BER_sim = np.zeros(len(pVec))
BLER_sim = np.zeros(len(pVec))
for j, p_value in enumerate(pVec):
BER_sim_sum = 0
BLER_sim_sum = 0
for _ in tqdm(prange(nSym), desc='N'):
# Message to encode
message = np.random.randint(2, size = k, dtype='int')
# Encode the message
encoded_message = np.dot(message, generator) % 2
# Add noise to the codeword
noise = np.random.choice([0, 'e'], size=(n,), p=[1-p_value, p_value])
recievedCodeword = np.array(['e' if noise[indx] == 'e' else encoded_message[indx] for indx in range(n)])
erasedBasis = np.delete(generator, np.where(recievedCodeword == 'e')[0], axis=1)
BLER_sim_sum += int(np.linalg.matrix_rank(GF(erasedBasis)) < erasedBasis.shape[0])
BLER_sim[j] = BLER_sim_sum / nSym
e_vec_bec[(n, k, 'bler')] = BLER_sim
rate = k / n
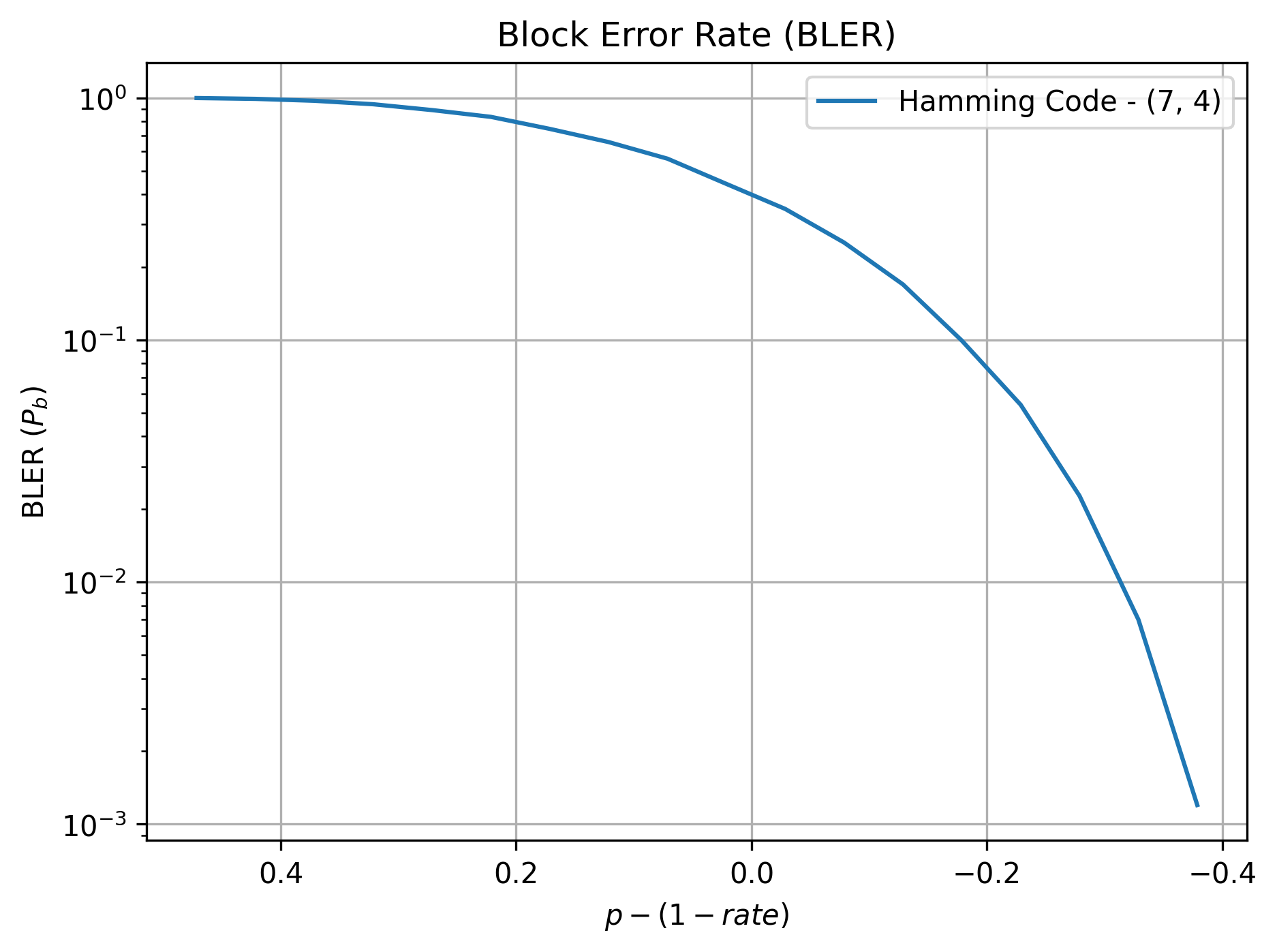
label = 'Hamming Code - (7, 4)'
fig, ax = plt.subplots()
plt.semilogy(pVec - (1- rate), e_vec_bec[(n, k, 'bler')], label=label)
ax.invert_xaxis()
ax.set_xlabel('$p - (1 - rate)$')
ax.set_ylabel('BLER ($P_b$)')
ax.set_title('Block Error Rate (BLER)')
ax.grid(True)
plt.tight_layout()
plt.legend()The plot is as follows: